絞り込む
第741号
2022.08.01
公的年金を考える(53)~物価上昇による影響~
令和4年に入って物価上昇が続いており、4月以降2%を超える月が続いている。今回はこうした物価上昇が年金制度にどのような影響を及ぼすのか、令和5年の年金額を予測することで考えてみたい。
1.令和4年度の年金額
令和4年度の年金額は、新規裁定・既裁定ともに名目手取り賃金変動率△0.4%により改定された。
| 令和3年度 | 令和4年度 | |
| 国民年金(老齢基礎年金)満額 | 65,075 円 | 64,816 円 |
| 厚生年金(老齢厚生年金)※ | 90,346 円 | 89,961 円 |
※平均的標準報酬(賞与込み)43.9万円で40年間就業の場合
年金額は、原則として新規裁定者(67歳以下)は名目手取り賃金変動率(以下、「賃金変動率))、既裁定者(67歳超)は物価変動率により改定されるが、賃金変動率が物価変動率を下回る場合は既裁定者も賃金変動率により改定される。(2021/4~)
| ケース | 新規裁定者 | 既裁定者 | |
| ① | 賃金変動率>物価変動率 | 賃金変動率 | 物価変動率 |
| ② | 物価変動率>賃金変動率 | 賃金変動率 | 賃金変動率 |
令和4年度年金額改定の前提数値は以下のとおりである。
- 令和3年物価変動率:△0.2%
- 賃金変動率:△0.4%
- マクロ経済スライド調整率:△0.3%
なお、マイナス改定のためマクロ経済スライドによる調整は行われずに、△0.3%は繰り越されている。
2.物価の動向
2000年以降の物価変動率(全国消費者物価指数)は以下のとおりである。
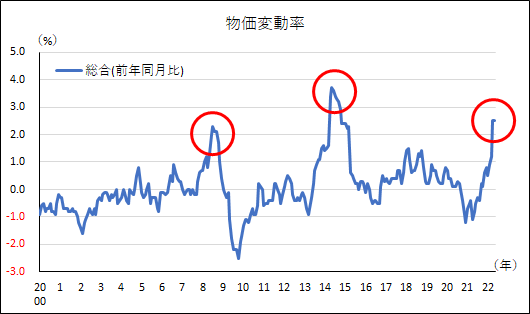
2000年以降、2%を超える上昇となったのは、2008年と2014年の2回しかない。2014年は消費税引上げが原因だが、2008年は原油価格や食料品価格の上昇により一時的に上昇したもののリーマンショックを契機とした世界的景気の落ち込みによって収束している。今回の物価上昇は、資源価格や原材料価格および円安によるものであり2008年とも類似するもののまだ収束の方向にはなく、当面は継続する可能性が高い。
3.令和5年度の年金額への影響
2022年の物価変動率が2.0%となった場合、既裁定者の年金額改定は、2.0%からマクロ経済スライドによる調整(繰越分を併せ△0.6%程度)を減じた率となり、1.4%程度の改定となる。(なお、賃金変動率が2.0%を超えることが条件となるが、超える公算が高い。)
この場合、年金額そのものは増加するものの物価には追い付かず実質的には減額となる。
ただし、年金額の実質的減少は保険料を引き上げないための施策として2004年法改正で導入された仕組みであり、物価の低迷によりこれまであまり機能していなかったものが、令和5年には上手く機能する、と考えるべきであろう。
(代表取締役・年金数理人 黒田英樹)
※JPACメールマガジン『年金・退職金レター』は、隔週で弊社コンサルタントが執筆いたします。
黒田 英樹 次回担当は2022年9月上旬の予定です。



